G. Toscani, M. Zanella

Preprint arXiv 2025

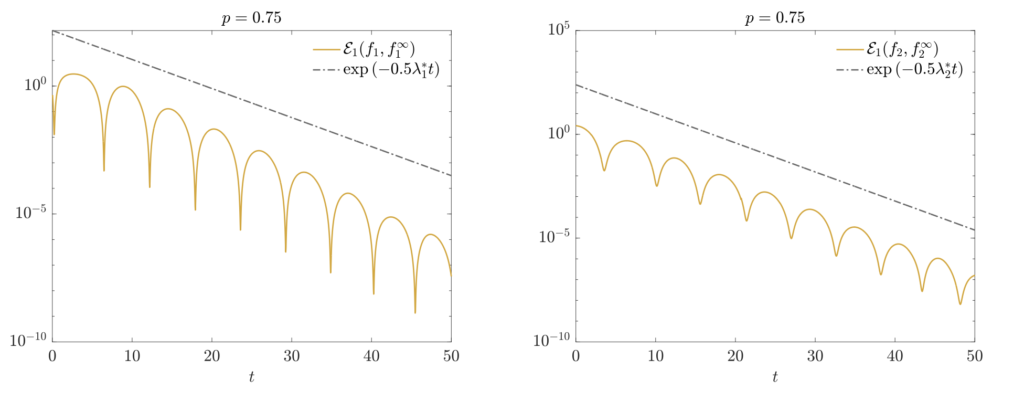
We study a system of Fokker-Planck equations recently introduced to describe the temporal evolution of statistical distributions of population densities with predator-prey interactions.

At the macroscopic level, the system recovers a Lotka-Volterra model and defines an explicit family of equilibrium densities that depend on the form of the diffusion coefficient. By introducing Energy-type distances, we rigorously establish exponential convergence to equilibrium in appropriate homogeneous Sobolev spaces, with a rate explicitly determined by the dissipative contribution of the interaction term. The analysis highlights the intrinsic energy dissipation mechanism governing the dynamics and clarifies how the evolution of expected quantities determines the emergence of a stable equilibrium configuration. This approach provides a new perspective on the convergence to equilibrium for problems with time-dependent coefficients.