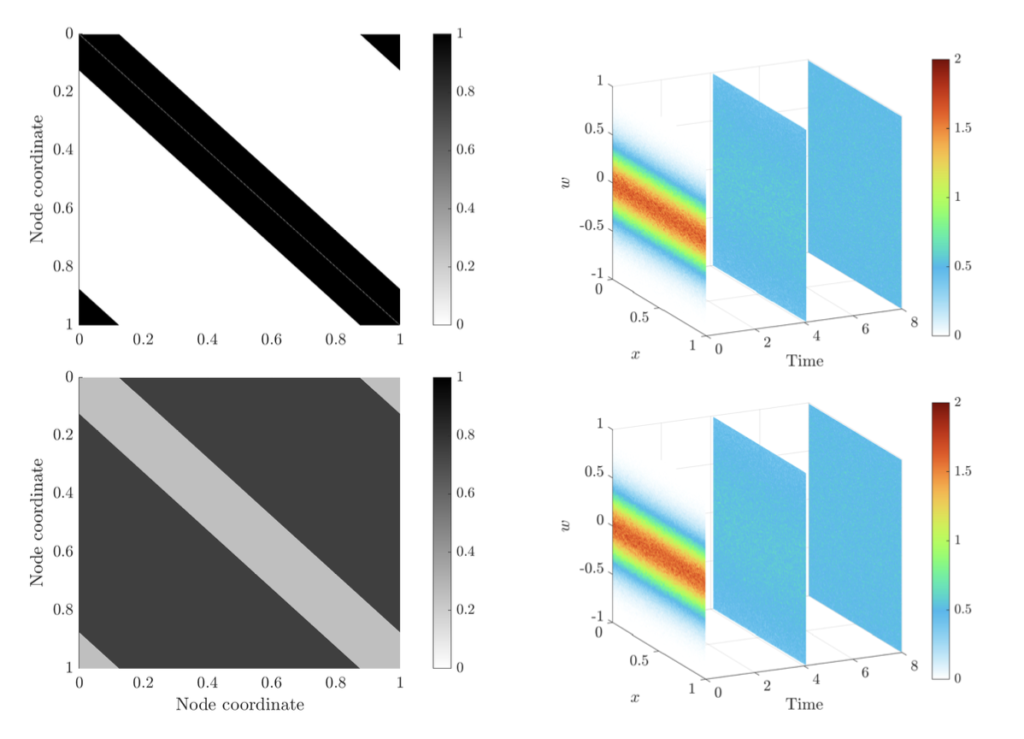
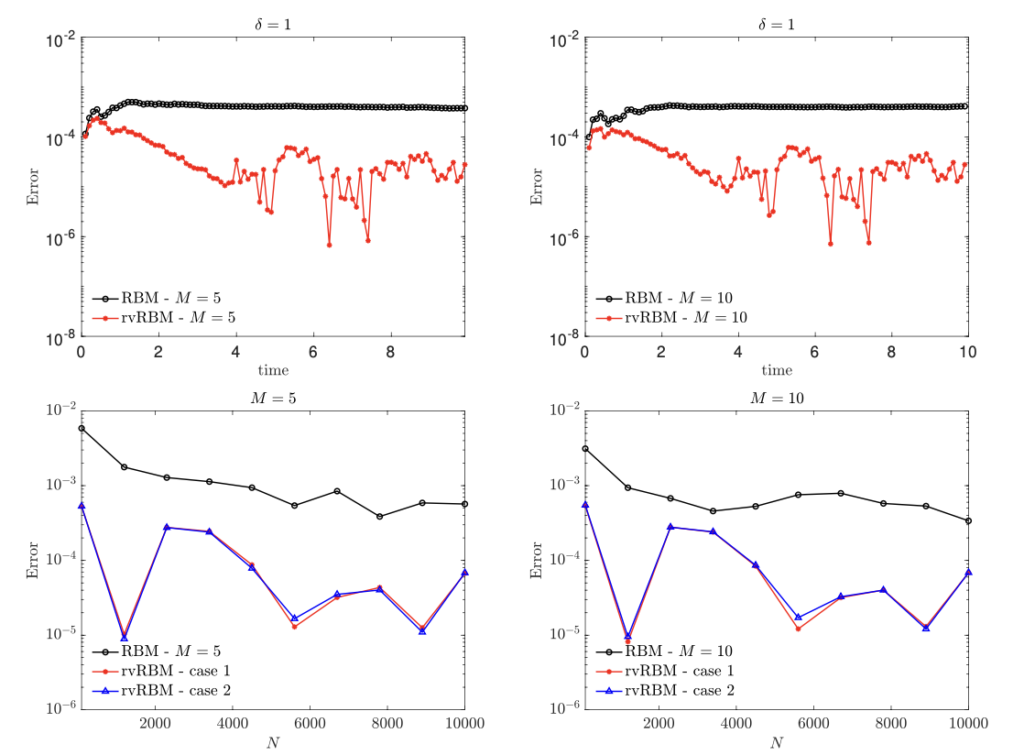
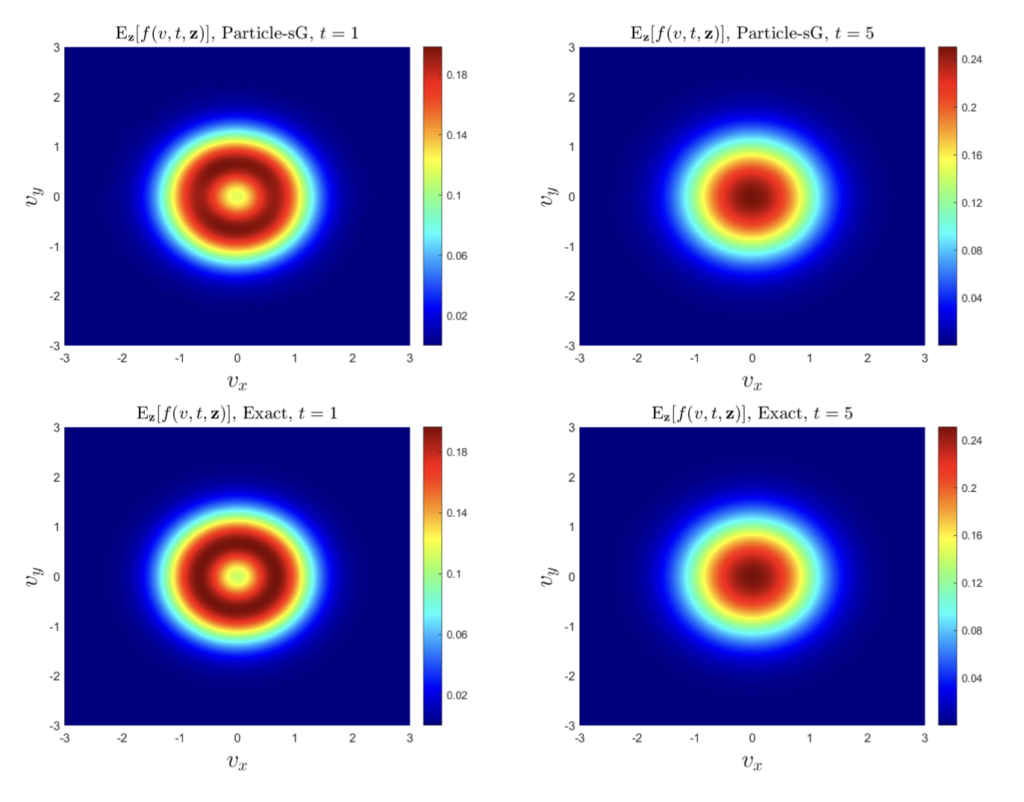
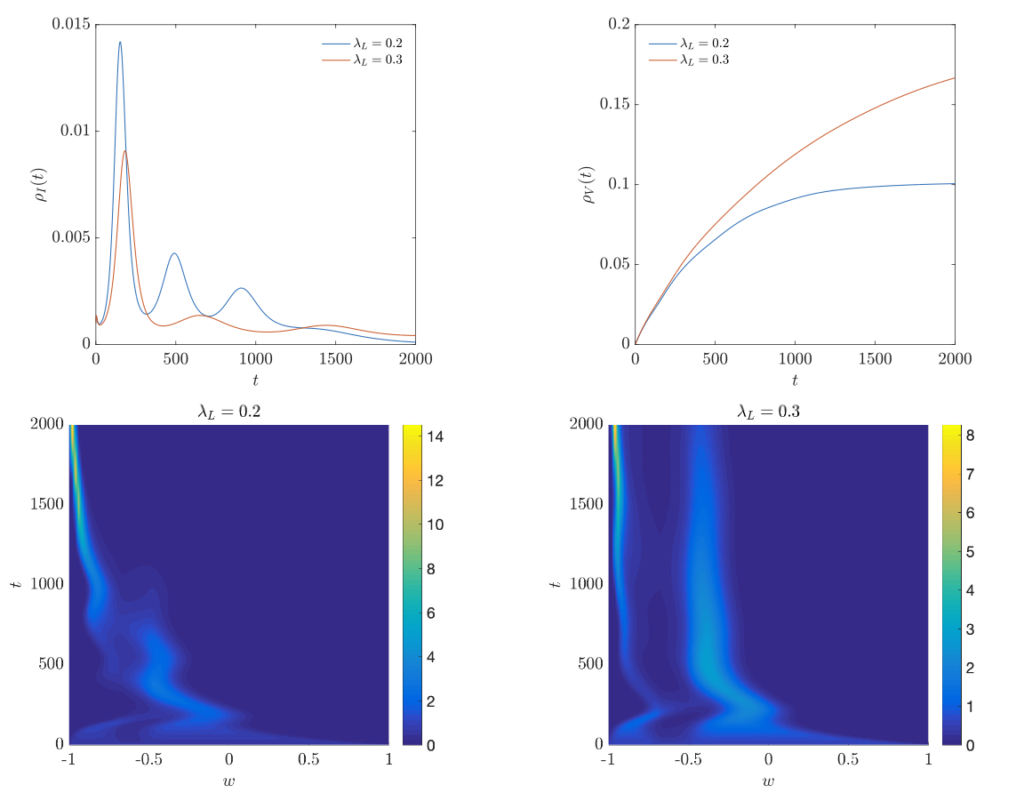
E. Calzola, G. Dimarco, G. Toscani, M. Zanella
Preprint arXiv, 2024
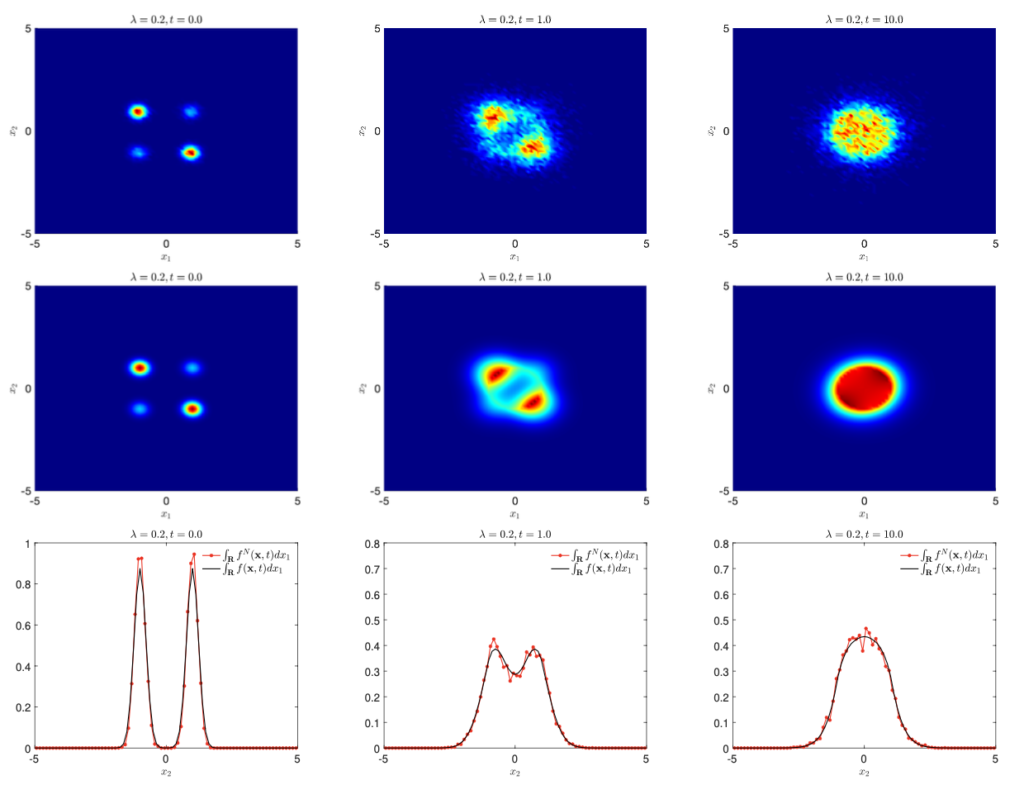
In this work, we define a class of models to understand the impact of population size on opinion formation dynamics, a phenomenon usually related to group conformity.
To this end, we introduce a new kinetic model in which the interaction frequency is weighted by the kinetic density. In the quasi-invariant regime, this model reduces to a Kaniadakis-Quarati-type equation with nonlinear drift, originally introduced for the dynamics of bosons in a spatially homogeneous setting. From the obtained PDE for the evolution of the opinion density, we determine the regime of parameters for which a critical mass exists and triggers blow-up of the solution. Therefore, the model is capable of describing strong conformity phenomena in cases where the total density of individuals holding a given opinion exceeds a fixed critical size. In the final part, several numerical experiments demonstrate the features of the introduced class of models and the related consensus effects.