Category Archives: Optimization and Control

Superlinear Drift in Consensus-Based Optimization with Condensation Phenomena

by Mattia Zanella

J. Franceschi, L. Pareschi, M. Zanella

Preprint arXiv, 2025

Consensus-based optimization (CBO) is a class of metaheuristic algorithms designed for global optimization problems. In the many-particle limit, classical CBO dynamics can be rigorously connected to mean-field equations that ensure convergence toward global minimizers under suitable conditions.

In this work, we draw inspiration from recent extensions of the Kaniadakis–Quarati model for indistinguishable bosons to develop a novel CBO method governed by a system of SDEs with superlinear drift and nonconstant diffusion. The resulting mean-field formulation in one dimension exhibits condensation-like phenomena, including finite-time blow-up and loss of L2-regularity. To avoid the curse of dimensionality a marginal based formulation which permits to leverage the one-dimensional results to multiple dimensions is proposed. We support our approach with numerical experiments that highlight both its consistency and potential performance improvements compared to classical CBO methods.

Kinetic simulated annealing optimization with entropy-based cooling rate

by Mattia Zanella

M. Herty, M. Zanella

Preprint arXiv, 2025

We present a modified simulated annealing method with a dynamical choice of the cooling temperature.

The latter is determined via a closed-loop control and is proven to yield exponential decay of the entropy of the particle system. The analysis is carried out through kinetic equations for interacting particle systems describing the simulated annealing method in an extended phase space. Decay estimates are derived under the quasi-invariant scaling of the resulting system of Boltzmann-type equations to assess the consistency with their mean-field limit. Numerical results are provided to illustrate and support the theoretical findings.

Control of Overpopulated Tails in Kinetic Epidemic Models

by Mattia Zanella

A. Medaglia, M. Zanella

Journal of Hyperbolic Differential Equations, in press. (Preprint arXiv)

We introduce model-based transition rates for controlled compartmental models in mathematical epidemiology, with a focus on the effects of control strategies applied to interacting multi-agent systems describing
contact formation dynamics.

In the framework of kinetic control problems, we compare two prototypical control protocols: one additive control directly influencing the dynamics and another targeting the interaction strength between agents. The emerging controlled macroscopic models are derived for an SIR compartmentalization to illustrate their impact on epidemic progression and contact interaction dynamics. Numerical results show the effectiveness of this approach in steering the dynamics and controlling epidemic trends, even in scenarios where contact distributions exhibit an overpopulated tail.

Understanding the Impact of Evaluation Metrics in Kinetic Models for Consensus-based Segmentation

by Mattia Zanella

R. F. Cabini, H. Tettamanti, M. Zanella.

Entropy, 27(2), 149, 2025. (Preprint arXiv)

In this article we extend a recently introduced kinetic model for consensus-based segmentation of images. In particular, we will interpret the set of pixels of a 2D image as an interacting particle system which evolves in time in view of a consensus-type process

obtained by interactions between pixels and external noise. Thanks to a kinetic formulation of the introduced model we derive the large time solution of the model. We will show that the choice of parameters defining the segmentation task can be chosen from a plurality of loss functions characterising the evaluation metrics.

Breaking consensus in kinetic opinion formation models on graphons

by Mattia Zanella

B. Düring, J. Franceschi, M.-T. Wolfram, M. Zanella

Journal of Nonlinear Science, 34:79,2024 . (Preprint arXiv)

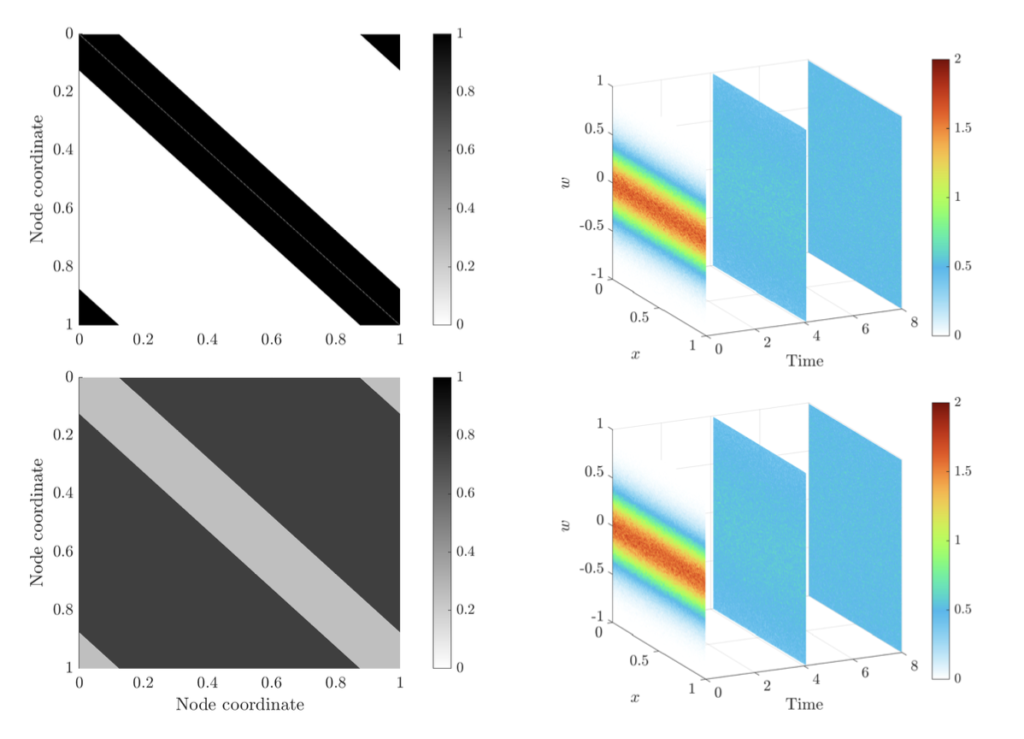
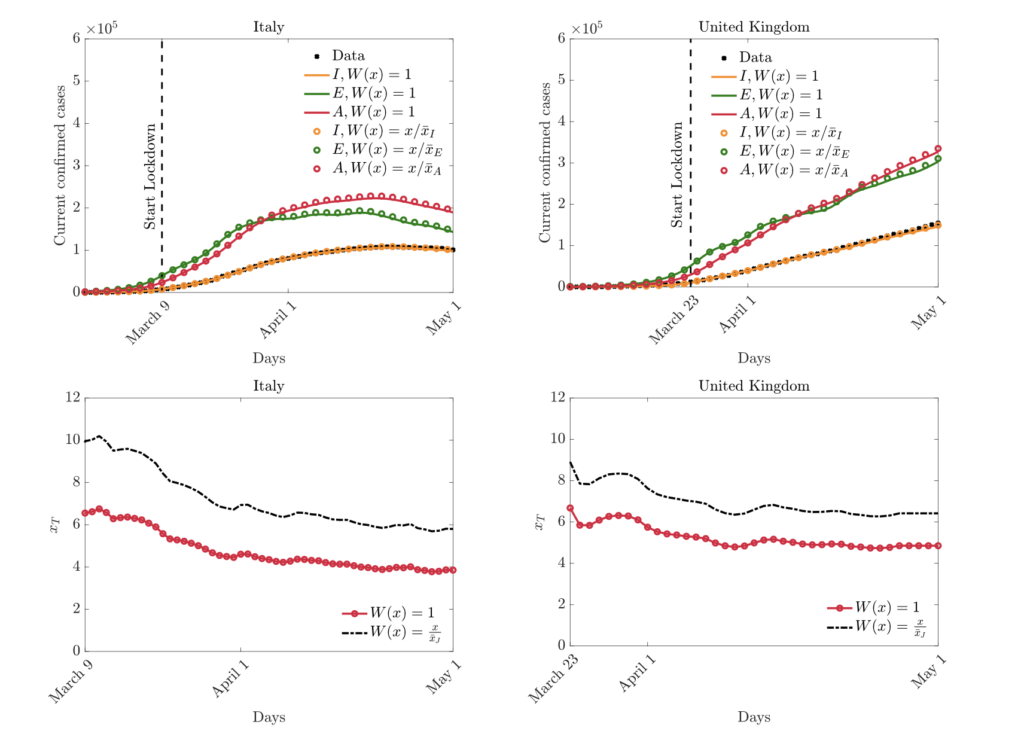
In this work we propose and investigate a strategy to prevent consensus in kinetic models for opinion formation. We consider a large interacting agent system, and assume that agent interactions are driven by compromise as well as self-thinking dynamics and also modulated by an underlying static social network.

This network structure is included using so-called graphons, which modulate the interaction frequency in the corresponding kinetic formulation. We then derive the corresponding limiting Fokker Planck equation, and analyze its large time behavior. This microscopic setting serves as a starting point for the proposed control strategy, which steers agents away from mean opinion and is characterised by a suitable penalization depending on the properties of the graphon. We show that this minimalist approach is very effective by analyzing the quasi-stationary solutions mean-field model in a plurality of graphon structures. Several numerical experiments are also provided the show the effectiveness of the approach in preventing the formation of consensus steering the system towards a declustered state.

On the optimal control of kinetic epidemic models with uncertain social features

by Mattia Zanella

J. Franceschi, A. Medaglia, M. Zanella.

Optim. Contr. Appl. Meth., 45(2): 494-522, 2024. (Preprint arXiv)

It is recognized that social heterogeneities in terms of the contact distribution have a strong influence on the spread of infectious diseases. Nevertheless, few data are available and their statistical description does not possess universal patterns and may vary spatially and temporally. It is therefore essential to design optimal control strategies, mimicking the effects of non-pharmaceutical interventions, to limit efficiently the number of infected cases.

In this work, starting from a recently introduced kinetic model for epidemiological dynamics that takes into account the impact of social contacts of individuals, we consider an uncertain contact formation dynamics leading to slim-tailed as well as fat-tailed distributions of contacts. Hence, we analyse the effects of an optimal control strategy of the system of agents. Thanks to classical methods of kinetic theory, we couple uncertainty quantification methods with the introduced mathematical model to assess the effects of social limitations. Finally, using the proposed modelling approach and starting from available data, we show the effectiveness of the proposed selective measures to dampen uncertainties together with the epidemic trends.

Uncertainty quantification and control of kinetic models for tumour growth under clinical uncertainties

by Mattia Zanella

A. Medaglia, G. Colelli, L. Farina, A. Bacila, P. Bini, E. Marchioni, S. Figini, A. Pichiecchio, M. Zanella

International Journal of Non-Linear Mechanics, 141:103933. (Preprint arXiv)

In this work, we develop a kinetic model for tumour growth taking into account the effects of clinical uncertainties characterising the tumours’ progression.

The action of therapeutic protocols trying to steer the tumours’ volume towards a target size is then investigated by means of suitable selective-type controls acting at the level of cellular dynamics. By means of classical tools of statistical mechanics for many-agent systems, we are able to prove that it is possible to dampen clinical uncertainties across the scales. To take into account the scarcity of clinical data and the possible source of error in the image segmentation of tumours’ evolution, we estimated empirical distributions of relevant parameters that are considered to calibrate the resulting model obtained from real cases of primary glioblastoma. Suitable numerical methods for uncertainty quantification of the resulting kinetic equations are discussed and, in the last part of the paper, we compare the effectiveness of the introduced control approaches in reducing the variability in tumours’ size due to the presence of uncertain quantities.

Kinetic modelling of epidemic dynamics: social contacts, control with uncertain data, and multiscale spatial dynamics

by Mattia Zanella

G. Albi, G. Bertaglia, W. Boscheri, G. Dimarco, L. Pareschi, G. Toscani, M. Zanella.

Predicting Pandemics in a Globally Connected World Vol.1, 2022. (Preprint arXiv)

In this survey we report some recent results in the mathematical modeling of epidemic phenomena through the use of kinetic equations.

We initially consider models of interaction between agents in which social characteristics play a key role in the spread of an epidemic, such as the age of individuals, the number of social contacts, and their economic wealth. Subsequently, for such models, we discuss the possibility of containing the epidemic through an appropriate optimal control formulation based on the policy maker’s perception of the progress of the epidemic. The role of uncertainty in the data is also discussed and addressed. Finally, the kinetic modeling is extended to spatially dependent settings using multiscale transport models that can characterize the impact of movement dynamics on epidemic advancement on both one-dimensional networks and realistic two-dimensional geographic settings.

Optimal control of epidemic spreading in the presence of social heterogeneity

by Mattia Zanella

G. Dimarco, G. Toscani, M. Zanella

Philosophical Transactions of the Royal Society A, 380:20210160, 2022. (Preprint arXiv)

The spread of COVID-19 has been thwarted in most countries through non-pharmaceutical interventions. In particular, the most effective measures in this direction have been the stay-at-home and closure strategies of businesses and schools.

However, population-wide lockdowns are far from being optimal carrying  heavy economic consequences. Therefore, there is nowadays a strong interest in designing more efficient restrictions. In this work, starting from a recent  kinetic-type model which takes into account the heterogeneity described by the social contact of individuals, we analyze the effects of introducing an optimal control strategy into the system, to limit selectively the mean number of contacts and reduce consequently the number of infected cases. Thanks to a data-driven approach, we show that this new mathematical model permits to assess the effects of the social limitations.  Finally, using the model introduced here and starting from the available data, we show the effectivity of the proposed selective measures to dampen the epidemic trends.

Kinetic-controlled hydrodynamics for multilane traffic models

by Mattia Zanella

R. Borsche, A. Klar, M. Zanella

Physica A: Statistical Mechanics and its Applications, 587: 126486, 2022. (Preprint arXiv)

We study the application of a recently introduced hierarchical description of traffic flow control by driver-assist vehicles to include lane changing dynamics. Lane-dependent feedback control strategies are implemented at the level of vehicles and the aggregate trends are studied by means of Boltzmann-type equations determining three different hydrodynamics based on the lane switching frequency. System of first order macroscopic equations describing the evolution of densities along the lanes are then consistently determined through a suitable closure strategy. Numerical examples are then presented to illustrate the features of the proposed hierarchical approach.