Category Archives: Numerical methods

Uncertainty quantification for charge transport in GNRs through particle Galerkin methods for the semiclassical Boltzmann equation

by Mattia Zanella

A. Medaglia, G. Nastasi, V. Romano, M. Zanella

Preprint arXiv, 2024.

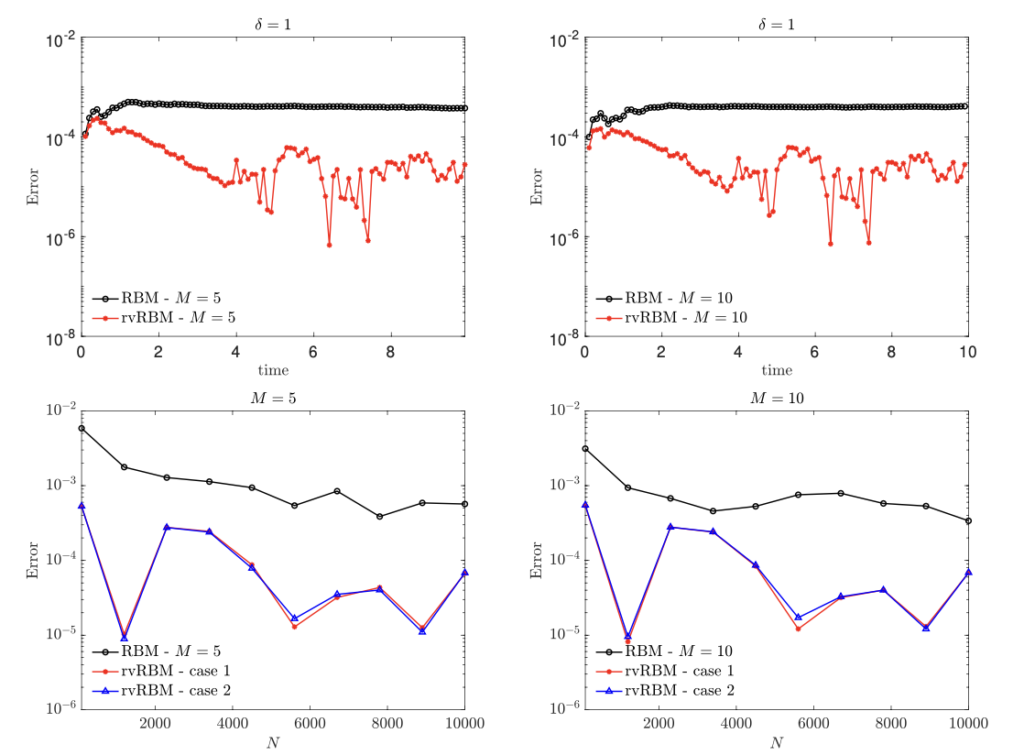
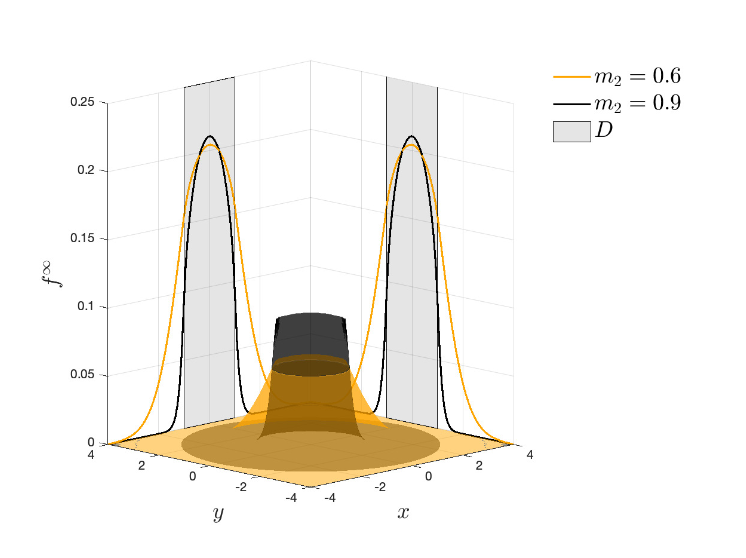
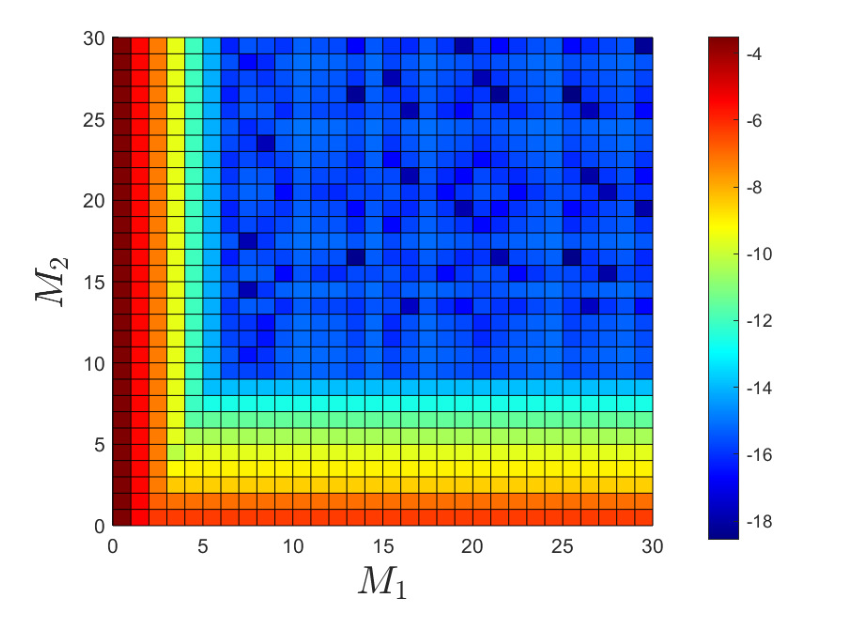
In this article, we investigate some issues related to the quantification of uncertainties associated with the electrical properties of graphene nanoribbons. The approach is suited to understand the effects of missing information linked to the difficulty of fixing some material parameters, such as the band gap, and the strength of the applied electric field. In particular, we focus on the extension of particle Galerkin methods for kinetic equations in the case of the semiclassical Boltzmann equation for charge transport in graphene nanoribbons with uncertainties. To this end, we develop an efficient particle scheme which allows us to parallelize the computation and then, after a suitable generalization of the scheme to the case of random inputs, we present a Galerkin reformulation of the particle dynamics, obtained by means of a generalized polynomial chaos approach, which allows the reconstruction of the kinetic distribution. As a consequence, the proposed particle-based scheme preserves the physical properties and the positivity of the distribution function also in the presence of a complex scattering in the transport equation of electrons. The impact of the uncertainty of the band gap and applied field on the electrical current is analyzed.

Reduced variance random batch methods for nonlocal PDEs

by Mattia Zanella

L. Pareschi, M. Zanella

Acta Appl. Math., 191, 4, 2024. (Preprint arXiv)

Random Batch Methods (RBM) for mean-field interacting particle systems enable the reduction of the quadratic computational cost associated with particle interactions to a near-linear cost. The essence of these algorithms lies in the random partitioning of the particle ensemble into smaller batches at each time step.

The interaction of each particle within these batches is then evolved until the subsequent time step. This approach effectively decreases the computational cost by an order of magnitude while increasing the amount of fluctuations due to the random partitioning. In this work, we propose a variance reduction technique for RBM applied to nonlocal PDEs of Fokker-Planck type based on a control variate strategy. The core idea is to construct a surrogate model that can be computed on the full set of particles at a linear cost while maintaining enough correlations with the original particle dynamics. Examples from models of collective behavior in opinion spreading and swarming dynamics demonstrate the great potential of the present approach.

Fokker-Planck modeling of many-agent systems in swarm manufacturing: asymptotic analysis and numerical results

by Mattia Zanella

F. Auricchio, G. Toscani, M. Zanella

Communications in Mathematical Sciences, 21(6):1655-1677, 2023. (Preprint arXiv)

In this paper we study a novel Fokker-Planck-type model that is designed to mimic manufacturing processes through the dynamics characterizing a large set of agents. In particular, we describe a many-agent system interacting with a target domain in such a way that each agent/particle is attracted by the center of mass of the target domain with the aim to uniformly cover this zone.

To this end, we first introduce a mean-field model with discontinuous flux whose large time behavior is such that the steady state is globally continuous and uniform over a connected portion of the domain. We prove that a diffusion coefficient that guarantees that a given portion of mass enters in the target domain exists and that it is unique. Furthermore, convergence to equilibrium in 1D is provided through a reformulation of the initial problem involving a nonconstant diffusion function. The extension to 2D is explored numerically by means of recently introduced structure preserving methods for Fokker-Planck equations.

Monte Carlo stochastic Galerkin methods for non-Maxwellian kinetic models of multiagent systems with uncertainties

by Mattia Zanella

A. Medaglia, A. Tosin, M. Zanella

Partial Differential Equations and Applications, 3, 51, 2022. (Preprint arXiv)

In this paper, we focus on the construction of a hybrid scheme for the approximation of non- Maxwellian kinetic models with uncertainties. In the context of multiagent systems, the introduction of a kernel at the kinetic level is useful to avoid unphysical interactions.

The methods here proposed, combine a direct simulation Monte Carlo (DSMC) in the phase space together with stochastic Galerkin (sG) methods in the random space. The developed schemes preserve the main physical properties of the solution together with accuracy in the random space. The consistency of the methods is tested with respect to surrogate Fokker-Planck models that can be obtained in the quasi-invariant regime of parameters. Several applications of the schemes to non-Maxwellian models of multiagent systems are reported.

Kinetic modelling of multiple interactions in socio-economic systems

by Mattia Zanella

Giuseppe Toscani, Andrea Tosin, Mattia Zanella

Network & Heterogeneous Media, 15(3): 519-542, 2020. (Preprint arXiv)

Unlike the classical kinetic theory of rarefied gases, where microscopic interactions among gas molecules are described as binary collisions, the modelling of socio-economic phenomena in a multi-agent system naturally requires to consider, in various situations, multiple interactions among the individuals. In this paper, we collect and discuss some examples related to economic and gambling activities. In particular, we focus on a linearisation strategy of the multiple interactions, which greatly simplifies the kinetic description of such systems while maintaining all their essential aggregate features, including the equilibrium distributions.

Structure preserving schemes for Fokker-Planck equations with nonconstant diffusion matrices

by Mattia Zanella

 

Nadia Loy, Mattia Zanella

Mathematics and Computers in Simulation, 188: 342-362, 2021. (Preprint arXiv)

In this work we consider an extension of a recently proposed structure preserving numerical scheme for nonlinear Fokker-Planck-type equations to the case of nonconstant full diffusion matrices. While in existing works the schemes are formulated in a one-dimensional setting, here we consider exclusively the two-dimensional case. We prove that the proposed schemes preserve fundamental structural properties like nonnegativity of the solution without restriction on the size of the mesh and entropy dissipation. Moreover, all the methods presented here are at least second order accurate in the transient regimes and arbitrarily high order for large times in the hypothesis in which the flux vanishes at the stationary state. Suitable numerical tests will confirm the theoretical results.

Hydrodynamic models of preference formation in multi-agent societies

by Mattia Zanella

Lorenzo Pareschi, Giuseppe Toscani, Andrea Tosin, Mattia Zanella

Journal of Nonlinear Science, 29(6): 2761-2796, 2019.  Preprint arXiv,

In this paper, we discuss the passage to hydrodynamic equations for kinetic models of opinion formation. The considered kinetic models feature an opinion density depending on an additional microscopic variable, identified with the personal preference. This variable describes an opinion-driven polarisation process, leading finally to a choice among some possible options, as it happens e.g. in referendums or elections. Like in the kinetic theory of rarefied gases, the derivation of hydrodynamic equations is essentially based on the computation of the local equilibrium distribution of the opinions from the underlying kinetic model. Several numerical examples validate the resulting model, shedding light on the crucial role played by the distinction between opinion and preference formation on the choice processes in multi-agent societies.

Kinetic-controlled hydrodynamics for traffic models with driver-assist vehicles

by Mattia Zanella

Andrea Tosin, Mattia Zanella

Multiscale Modeling and Simulation, 17(2): 716-749, 2019. (Preprint arXiv)

We develop a hierarchical description of traffic flow control by means of driver-assist vehicles aimed at the mitigation of speed-dependent road risk factors. Microscopic feedback control strategies are designed at the level of vehicle-to-vehicle interactions and then upscaled to the global flow via a kinetic approach based on a Boltzmann-type equation. Then first and second order hydrodynamic traffic models, which naturally embed the microscopic control strategies, are consistently derived from the kinetic-controlled framework via suitable closure methods. Several numerical examples illustrate the effectiveness of such a hierarchical approach at the various scales.

 

Particle based gPC methods for mean-field models of swarming with uncertainty

by Mattia Zanella

José Antonio Carrillo, Lorenzo Pareschi, Mattia Zanella.

Communications in Computational Physics, 25(2): 508-531, 2019. (Preprint arXiv)

In this work we focus on the construction of numerical schemes for the approximation of stochastic mean–field equations which preserve the nonnegativity of the solution. The method here developed makes use of a mean-field Monte Carlo method in the physical variables combined with a generalized Polynomial Chaos (gPC) expansion in the random space. In contrast to a direct application of stochastic-Galerkin methods, which are highly accurate but lead to the loss of positivity, the proposed schemes are capable to achieve high accuracy in the random space without loosing nonnegativity of the solution. Several applications of the schemes to mean-field models of collective behavior are reported.

 

See more videos on my YouTube channel.

Uncertainty quantification for kinetic models in socio-economic and life sciences

by Mattia Zanella

Giacomo Dimarco, Lorenzo Pareschi, Mattia Zanella  

Uncertainty Quantification for Hyperbolic and Kinetic Equations, Eds. S. Jin, L. Pareschi, SEMA-SIMAI Springer Series vol.14, Springer-Cham, 2017. (Preprint arXiv)

Kinetic equations play a major rule in modeling large systems of interacting particles. Recently the legacy of classical kinetic theory found novel applications in socio-economic and life sciences, where processes characterized by large groups of agents exhibit spontaneous emergence of social structures. Well-known examples are the formation of clusters in opinion dynamics, the appearance of inequalities in wealth distributions, flocking and milling behaviors in swarming models, synchronization phenomena in biological systems and lane formation in pedestrian traffic. The construction of kinetic models describing the above processes, however, has to face the difficulty of the lack of fundamental principles since physical forces are replaced by empirical social forces. These empirical forces are typically constructed with the aim to reproduce qualitatively the observed system behaviors, like the emergence of social structures, and are at best known in terms of statistical information of the modeling parameters. For this reason the presence of random inputs characterizing the parameters uncertainty should be considered as an essential feature in the modeling process. In this survey we introduce several examples of such kinetic models, that are mathematically described by nonlinear Vlasov and Fokker–Planck equations, and present different numerical approaches for uncertainty quantification which preserve the main features of the kinetic solution.