L. Pareschi, M. Zanella

Preprint arXiv, 2023

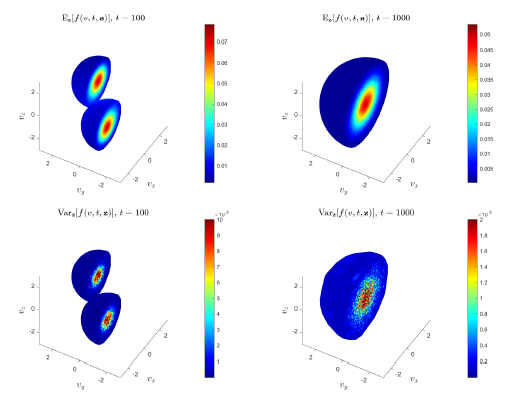
Random Batch Methods (RBM) for mean-field interacting particle systems enable the reduction of the quadratic computational cost associated with particle interactions to a near-linear cost. The essence of these algorithms lies in the random partitioning of the particle ensemble into smaller batches at each time step.

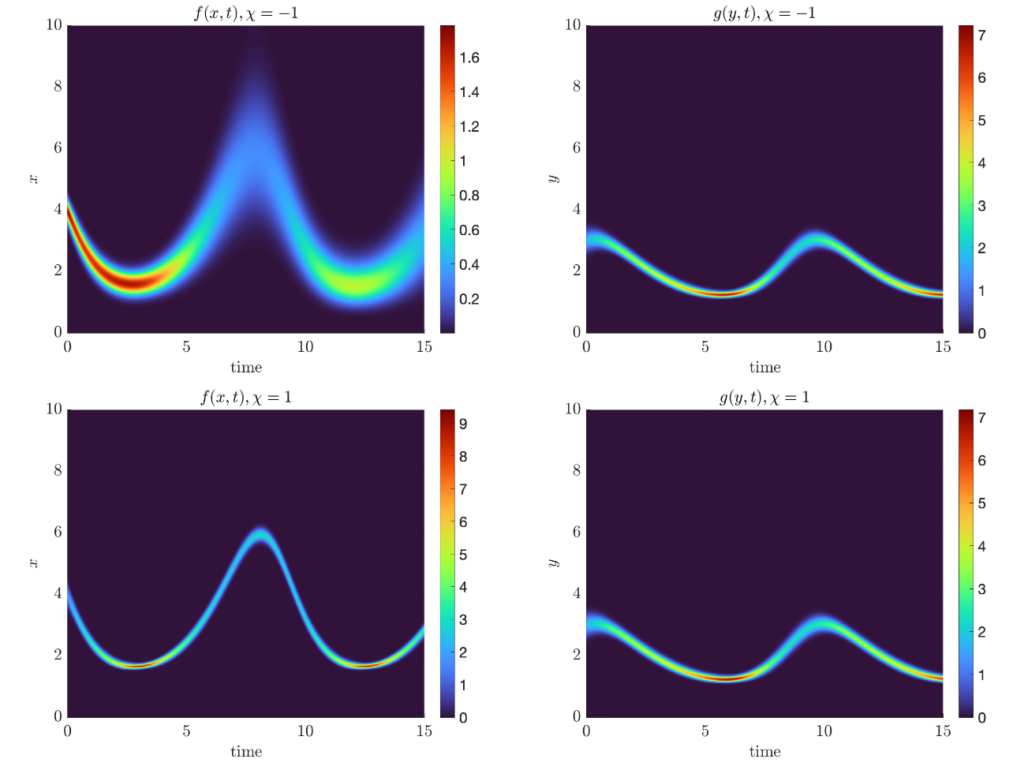
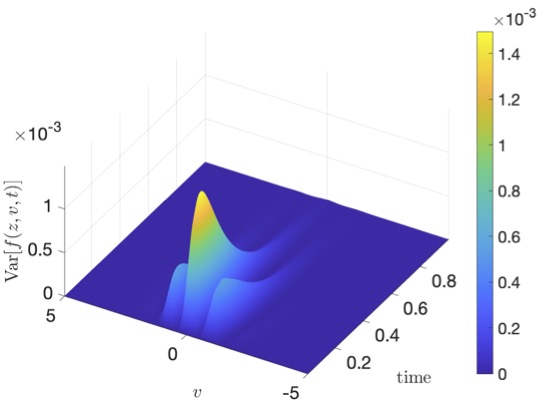
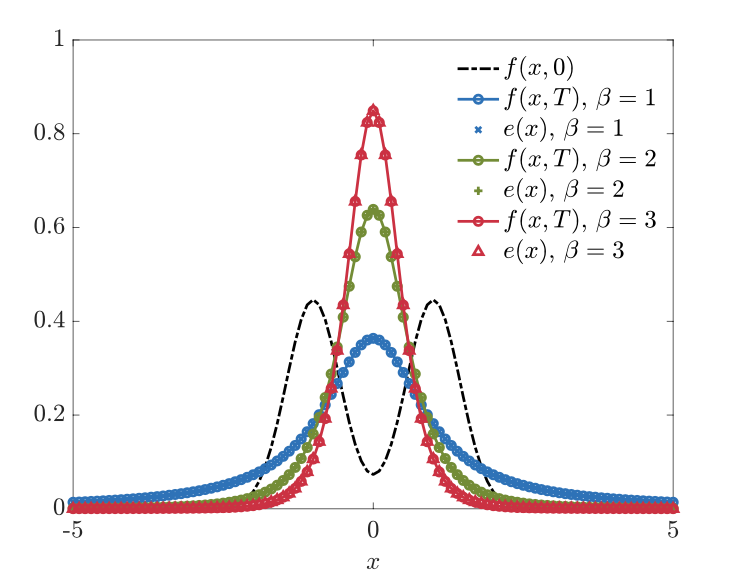
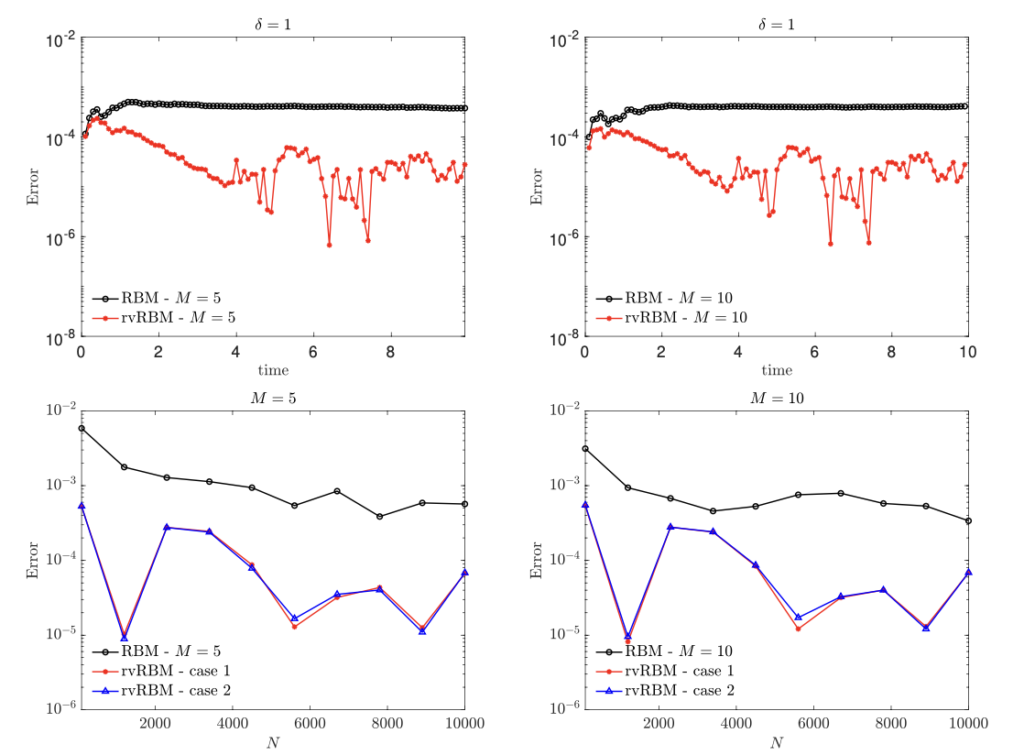
The interaction of each particle within these batches is then evolved until the subsequent time step. This approach effectively decreases the computational cost by an order of magnitude while increasing the amount of fluctuations due to the random partitioning. In this work, we propose a variance reduction technique for RBM applied to nonlocal PDEs of Fokker-Planck type based on a control variate strategy. The core idea is to construct a surrogate model that can be computed on the full set of particles at a linear cost while maintaining enough correlations with the original particle dynamics. Examples from models of collective behavior in opinion spreading and swarming dynamics demonstrate the great potential of the present approach.

G. Toscani, M. Zanella

Rivista di Matematica della Università di Parma, in press. (Preprint arXiv)

Owing to the analogies between the problem of wealth redistribution with taxation in a multi-agent society, we introduce and discuss a kinetic model describing the statistical distributions in time of the sizes of groups of biological systems with prey-predator dynamics.

While the evolution of the mean values is shown to be driven by a classical Lotka-Volterra system of differential equations, it is shown that the time evolution of the probability distributions of the size of groups of the two interacting species is heavily dependent both on a kinetic redistribution operator and the degree of randomness present in the system. Numerical experiments are given to clarify the time-behavior of the distributions of groups of the species.

G. Dimarco, L. Pareschi, M. Zanella.

Multiscale Modeling & Simulation, in press. (Preprint arXiv)

Nonlinear Fokker-Planck equations play a major role in modeling large systems of interacting particles with a proved effectiveness in describing real world phenomena ranging from classical fields such as fluids and plasma to social and biological dynamics.

Their mathematical formulation has often to face with physical forces having a significant random component or with particles living in a random environment which characterization may be deduced through experimental data and leading consequently to uncertainty-dependent equilibrium states. In this work, to address the problem of effectively solving stochastic Fokker-Planck systems, we will construct a new equilibrium preserving scheme through a micro-macro approach based on stochastic Galerkin methods. The resulting numerical method, contrarily to the direct application of a stochastic Galerkin projection in the parameter space of the unknowns of the underlying
Fokker-Planck model, leads to highly accurate description of the uncertainty dependent large time behavior. Several numerical tests in the context of collective behavior for social and life sciences are presented to assess the validity of the present methodology against standard ones.

G. Toscani, M. Zanella

Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl., 32:471-496, 2021. (Preprint arXiv)

We study the relaxation to equilibrium for a class linear one-dimensional Fokker-Planck equations characterized by a particular subcritical confinement potential.

An interesting feature of this class of Fokker-Planck equations is that, for any given probability density $e(x)$, the diffusion coefficient can be built to have $e(x)$ as steady state. This representation of the equilibrium density can be fruitfully used to obtain one-dimensional Wirtinger-type inequalities and to recover, for a sufficiently regular density $e(x) $, a polynomial rate of convergence to equilibrium.Numerical results then confirm the theoretical analysis, and allow to conjecture that convergence to equilibrium with positive rate still holds for steady states characterized by a very slow polynomial decay at infinity.