Mattia Zanella

Mathematics and Computers in Simulation,  168:28-47, 2020. (Preprint arXiv)

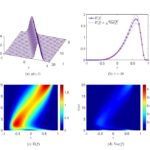
This paper is devoted to the construction of structure preserving stochastic Galerkin schemes for Fokker-Planck type equations with uncertainties and interacting with an external distribution called the background. The proposed methods are capable to preserve physical properties in the approximation of statistical moments of the problem like nonnegativity, entropy dissipation and asymptotic behaviour of the expected solution. The introduced methods are second order accurate in the transient regimes and high order for large times. We present applications of the developed schemes to the case of fixed and dynamic background distribution for models of collective behaviour.