 G. Dimarco, A. Tosin, M. Zanella
G. Dimarco, A. Tosin, M. Zanella
Journal of Statistical Physics, 186, 17, 2022. (Preprint arXiv)
In this paper, we derive second order hydrodynamic traffic models from kinetic-controlled equations for driver-assist vehicles. At the vehicle level we take into account two main control strategies synthesising the action of adaptive cruise controls and cooperative adaptive cruise controls. The resulting macroscopic dynamics fulfil the anisotropy condition introduced in the celebrated Aw-Rascle-Zhang model. Unlike other models based on heuristic arguments, our approach unveils the main physical aspects behind frequently used hydrodynamic traffic models and justifies the structure of the resulting macroscopic equations incorporating driver-assist vehicles. Numerical insights show that the presence of driver-assist vehicles produces an aggregate homogenisation of the mean flow speed, hich may also be steered towards a suitable desired speed in such a way that optimal flows and traffic stabilisation are reached
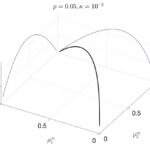 R. Borsche, A. Klar, M. Zanella
R. Borsche, A. Klar, M. Zanella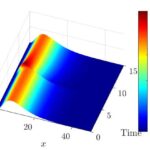 G. Dimarco, B. Perthame, G. Toscani, M. Zanella
G. Dimarco, B. Perthame, G. Toscani, M. Zanella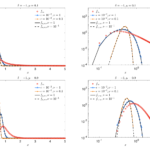
 G. Albi, L. Pareschi, M. Zanella
G. Albi, L. Pareschi, M. Zanella G. Albi, L. Pareschi, M. Zanella
G. Albi, L. Pareschi, M. Zanella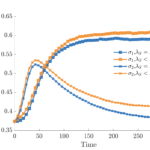 G. Dimarco, L. Pareschi, G. Toscani, M. Zanella
G. Dimarco, L. Pareschi, G. Toscani, M. Zanella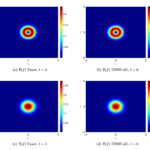
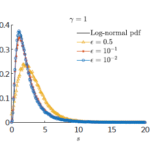 Andrea Tosin, Mattia Zanella
Andrea Tosin, Mattia Zanella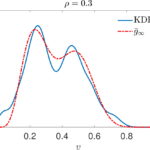 Michael Herty, Andrea Tosin, Giuseppe Visconti, Mattia Zanella
Michael Herty, Andrea Tosin, Giuseppe Visconti, Mattia Zanella