T. Lorenzi, H. Tettamanti, M. Zanella

Preprint arXiv, 2025

We present a new class of models for assessing the cell dynamics characterising muscular dystrophies. The proposed approach comprises a system of integro-differential equations for the statistical distributions

over a large patient cohort, of the densities of muscle fibers and immune cells implicated in muscle inflammation, degeneration, and regeneration, which underpin disease development. Considering an appropriately scaled version of this model, we formally derive, as the corresponding mean-field limit, a system of Fokker-Planck equations, from which we subsequently derive, as a macroscopic model counterpart, a system of differential equations for the mean densities of muscle and immune cells in the cohort of patients and the related variances. Then, we study long-time asymptotics for the mean-field
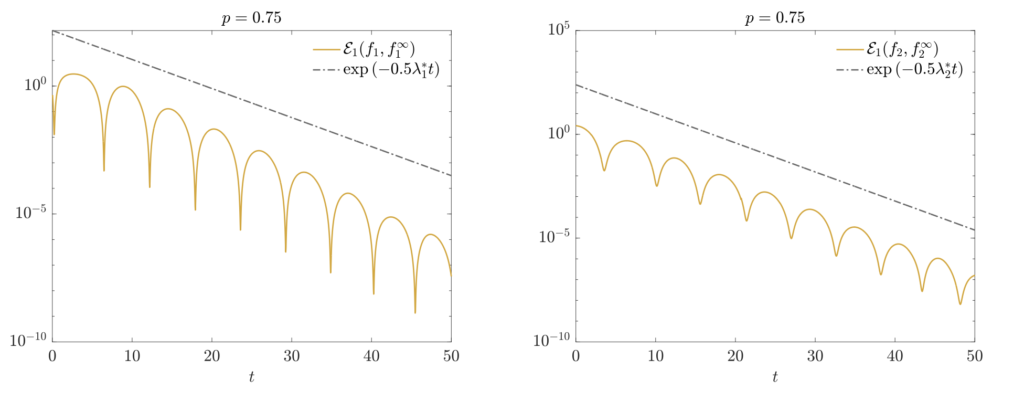
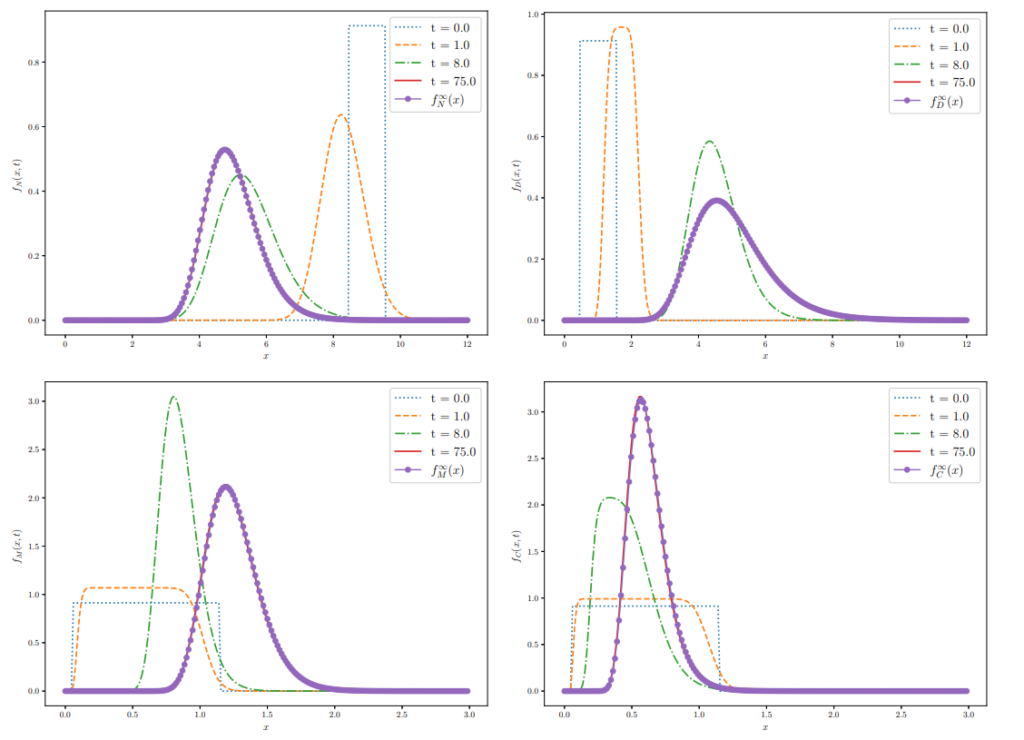
model by determining the quasi-equilibrium cell distribution functions, which are in the form of probability density functions of inverse Gamma distributions, and proving the long-time convergence to such quasi-equilibrium distributions. The analytical results obtained are illustrated by means of a sample of results of numerical simulations. The modeling approach presented here has the potential to offer new insights into the balance between degeneration and regeneration mechanisms in the progression of muscular dystrophies, and provides a basis for future extensions, including the modeling of therapeutic interventions.

G. Toscani, M. Zanella

Preprint arXiv 2025

We study a system of Fokker-Planck equations recently introduced to describe the temporal evolution of statistical distributions of population densities with predator-prey interactions.

At the macroscopic level, the system recovers a Lotka-Volterra model and defines an explicit family of equilibrium densities that depend on the form of the diffusion coefficient. By introducing Energy-type distances, we rigorously establish exponential convergence to equilibrium in appropriate homogeneous Sobolev spaces, with a rate explicitly determined by the dissipative contribution of the interaction term. The analysis highlights the intrinsic energy dissipation mechanism governing the dynamics and clarifies how the evolution of expected quantities determines the emergence of a stable equilibrium configuration. This approach provides a new perspective on the convergence to equilibrium for problems with time-dependent coefficients.

A. Bondesan, M. Menale, G. Toscani, M. Zanella.

Nonlinearity, in press. (Preprint arXiv)

In this work, we examine a kinetic framework for modeling the time evolution of size distribution densities of two populations governed by predator–prey interactions. The model builds upon the classical Boltzmann-type equations, where the dynamics arise from elementary binary interactions between the populations.

The model uniquely incorporates a linear redistribution operator to quantify the birth rates in both populations, inspired by wealth redistribution operators. We prove that, under a suitable scaling regime, the Boltzmann formulation transitions to a system of coupled Fokker–Planck-type equations. These equations describe the evolution of the distribution densities and link the macroscopic dynamics of their mean values to a Lotka–Volterra system of ordinary differential equations, with parameters explicitly derived from the microscopic interaction rules. We then determine the local equilibria of the Fokker–Planck system, which are Gamma-type densities, and investigate the problem of relaxation of its solutions toward these kinetic equilibria, in terms of their moments’ dynamics. The results establish a bridge between kinetic modeling and classical population dynamics, offering a multiscale perspective on predator–prey systems.

G. Toscani, M. Zanella

Ricerche di Matematica, 2025.

(Preprint arXiv)

We study the main properties of the solution of a Fokker-Planck equation characterized by a variable diffusion coefficient and a polynomial superlinear drift, modeling the formation of consensus in a large interacting system of individuals.

The Fokker-Planck equation is derived from the kinetic description of the dynamics of a quantum particle system, and in presence of a high nonlinearity in the drift operator, mimicking the effects of the mass in the alignment forces, allows for steady states similar to a Bose-Einstein condensate. The analysis shows that the regularity of the solution is strongly linked to the degree of nonlinearity in the drift, and that finite-time blow-up of the solution can occur when the degree of nonlinearity is sufficiently high. However, the presence of diffusion prevents the solution from forming condensation after the blow-up time.