Category Archives: Uncertainty Quantification

Mean-field control variate methods for kinetic equations with uncertainties and applications to socio-economic sciences

by Mattia Zanella

L. Pareschi, T. Trimborn, M. Zanella

International Journal for Uncertainty Quantification, 12(1): 61-84, 2022. (Preprint arXiv)

In this paper, we extend a recently introduced multi-fidelity control variate for the uncertainty quantification of the Boltzmann equation to the case of kinetic models arising in the study of multiagent systems. For these phenomena, where the effect of uncertainties is particularly evident, several models have been developed whose equilibrium states are typically unknown. In particular, we aim to develop efficient numerical methods based on solving the kinetic equations in the phase space by Direct Simulation Monte Carlo (DSMC) coupled to a Monte Carlo sampling in the random space. To this end, exploiting the knowledge of the corresponding mean-field approximation we develop novel mean-field Control Variate (MFCV) methods that are able to strongly reduce the variance of the standard Monte Carlo sampling method in the random space. We verify these observations with several numerical examples based on classical models , including wealth exchanges and opinion formation model for collective phenomena.

Modelling lockdown measures in epidemic outbreaks using selective socio-economic containment with uncertainty.

by Mattia Zanella

G. Albi, L. Pareschi, M. Zanella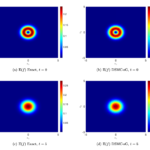

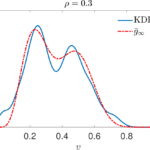Mathematical Biosciences and Engineering, 18(6): 7161-7190, 2021. (Preprint arXiv)

After the introduction of drastic containment measures aimed at stopping the epidemic contagion from SARS-CoV2, many governments have adopted a strategy based on a periodic relaxation of such measures in the face of a severe economic crisis caused by lockdowns. Assessing the impact of such openings in relation to the risk of a resumption of the spread of the disease is an extremely difficult problem due to the many unknowns concerning the actual number of people infected, the actual reproduction number and infection fatality rate of the disease. In this work, starting from a compartmental model with a social structure and stochastic inputs, we derive models with multiple feedback controls depending on the social activities that allow to assess the impact of a selective relaxation of the containment measures in the presence of uncertain data. Specific contact patterns in the home, work, school and other locations have been considered. Results from different scenarios concerning the first wave of the epidemic in some major countries, including Germany, France, Italy, Spain, the United Kingdom and the United States, are presented and discussed.

Monte Carlo stochastic Galerkin methods for the Boltzmann equation with uncertainties: space-homogeneous case

by Mattia Zanella

Lorenzo Pareschi, Mattia Zanella

Journal of Computational Physics, 423: 109822, 2020. (Preprint arXiv)

In this paper we propose a novel numerical approach for the Boltzmann equation with uncertainties. The method combines the efficiency of classical direct simulation Monte Carlo (DSMC) schemes in the phase space together with the accuracy of stochastic Galerkin (sG) methods in the random space. This  hybrid formulation makes it possible to construct methods that preserve the main physical properties of the solution along with spectral accuracy in the random space. The schemes are developed and analyzed in the case of space homogeneous problems as these contain the main numerical difficulties. Several test cases are reported, both in the Maxwell and in the variable hard sphere (VHS) framework, and confirm the properties and performance of the new methods.

 

Reconstruction of traffic speed distributions from kinetic models with uncertainties

by Mattia Zanella

Michael Herty, Andrea Tosin, Giuseppe Visconti, Mattia Zanella

Mathematical descriptions of traffic flow: micro, macro and kinetic models, pp. 1-16. (Preprint arXiv)

In this work we investigate the ability of a kinetic approach for traffic dynamics to predict speed distributions obtained through rough data. The present approach adopts the formalism of uncertainty quantification, since reaction strengths are uncertain and linked to different types of driver behaviour or different classes of vehicles present in the flow. Therefore, the calibration of the expected speed distribution has to face the reconstruction of the distribution of the uncertainty. We adopt experimental microscopic measurements recorded on a German motorway, whose speed distribution shows a multimodal trend. The calibration is performed by extrapolating the uncertainty parameters of the kinetic distribution via a constrained optimisation approach. The results confirm the validity of the theoretical set-up.

Uncertainty damping in kinetic traffic models by driver-assist controls

by Mattia Zanella

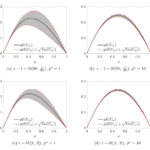Andrea Tosin, Mattia Zanella

Mathematical Control and Related Fields, 11(3): 681-713, 2021. (Preprint arXiv)

In this paper, we propose a kinetic model of traffic flow with uncertain binary interactions, which explains the scattering of the fundamental diagram in terms of the macroscopic variability of aggregate quantities, such as the mean speed and the flux of the vehicles, produced by the microscopic uncertainty. Moreover, we design control strategies at the level of the microscopic interactions among the vehicles, by which we prove that it is possible to dampen the propagation of such an uncertainty across the scales. Our analytical and numerical results suggest that the aggregate traffic flow may be made more ordered, hence predictable, by implementing such control protocols in driver-assist vehicles. Remarkably, they also provide a precise relationship between a measure of the macroscopic damping of the uncertainty and the penetration rate of the driver-assist technology in the traffic stream.

 

Monte Carlo gPC methods for diffusive kinetic flocking models with uncertainties

by Mattia Zanella

José Antonio Carrillo, Mattia Zanella

Vietnam Journal of Mathematics, 47(4):931-954, 2019. (Preprint arXiv)

In this paper we introduce and discuss numerical schemes for the approximation of kinetic equations for flocking behavior with phase transitions that incorporate uncertain quantities. This class of schemes here considered make use of a Monte Carlo approach in the phase space coupled with a stochastic Galerkin expansion in the random space. The proposed methods naturally preserve the positivity of the statistical moments of the solution and are capable to achieve high accuracy in the random space. Several tests on a kinetic alignment model with self propulsion validate the proposed methods both in the homogeneous and inhomogeneous setting, shading light on the influence of uncertainties in phase transition phenomena driven by noise such as their smoothing and confidence bands.

 

Structure preserving stochastic Galerkin methods for Fokker-Planck equations with background interactions

by Mattia Zanella

Mattia Zanella

Mathematics and Computers in Simulation,  168:28-47, 2020. (Preprint arXiv)

This paper is devoted to the construction of structure preserving stochastic Galerkin schemes for Fokker-Planck type equations with uncertainties and interacting with an external distribution called the background. The proposed methods are capable to preserve physical properties in the approximation of statistical moments of the problem like nonnegativity, entropy dissipation and asymptotic behaviour of the expected solution. The introduced methods are second order accurate in the transient regimes and high order for large times. We present applications of the developed schemes to the case of fixed and dynamic background distribution for models of collective behaviour.

 

Particle based gPC methods for mean-field models of swarming with uncertainty

by Mattia Zanella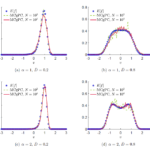

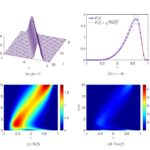
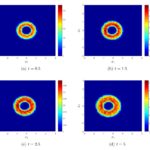José Antonio Carrillo, Lorenzo Pareschi, Mattia Zanella.

Communications in Computational Physics, 25(2): 508-531, 2019. (Preprint arXiv)

In this work we focus on the construction of numerical schemes for the approximation of stochastic mean–field equations which preserve the nonnegativity of the solution. The method here developed makes use of a mean-field Monte Carlo method in the physical variables combined with a generalized Polynomial Chaos (gPC) expansion in the random space. In contrast to a direct application of stochastic-Galerkin methods, which are highly accurate but lead to the loss of positivity, the proposed schemes are capable to achieve high accuracy in the random space without loosing nonnegativity of the solution. Several applications of the schemes to mean-field models of collective behavior are reported.

 

See more videos on my YouTube channel.

Hybrid stochastic kinetic description of two-dimensional traffic dynamics

by Mattia Zanella

Michael Herty, Andrea Tosin, Giuseppe Visconti, Mattia Zanella

SIAM Journal on Applied Mathematics, 78(5): 2737–2762, 2018. (Preprint arXiv)

In this work we present a two-dimensional kinetic traffic model which takes into account speed changes both when vehicles interact along the road lanes and when they change lane. Assuming that lane changes are less frequent than interactions along the same lane and considering that their mathematical description can be done up to some uncertainty in the model parameters, we derive a hybrid stochastic Fokker-Planck-Boltzmann equation in the quasi-invariant interaction limit. By means of suitable numerical methods, precisely structure preserving and direct Monte Carlo schemes, we use this equation to compute theoretical speed-density diagrams of traffic both along and across the lanes, including estimates of the data dispersion, and validate them against real data.

Boltzmann-type models with uncertain binary interactions

by Mattia Zanella

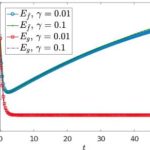Andrea Tosin, Mattia Zanella.

Communications in Mathematical Sciences, 16(4): 963-985, 2018. (Preprint arXiv)

In this paper we study binary interaction schemes with uncertain parameters for a general class of Boltzmann-type equations with applications in classical gas and aggregation dynamics. We consider deterministic (i.e., a priori averaged) and stochastic kinetic models, corresponding to different ways of understanding the role of uncertainty in the system dynamics, and compare some thermodynamic quantities of interest, such as the mean and the energy, which characterise the asymptotic trends. Furthermore, via suitable scaling techniques we derive the corresponding deterministic and stochastic Fokker-Planck equations in order to gain more detailed insights into the respective asymptotic distributions. We also provide numerical evidences of the trends estimated theoretically by resorting to recently introduced structure preserving uncertainty quantification methods.