A. Medaglia, L. Pareschi, M. Zanella
J. Comput. Phys., 503:112845, 2024. (Preprint arXiv)
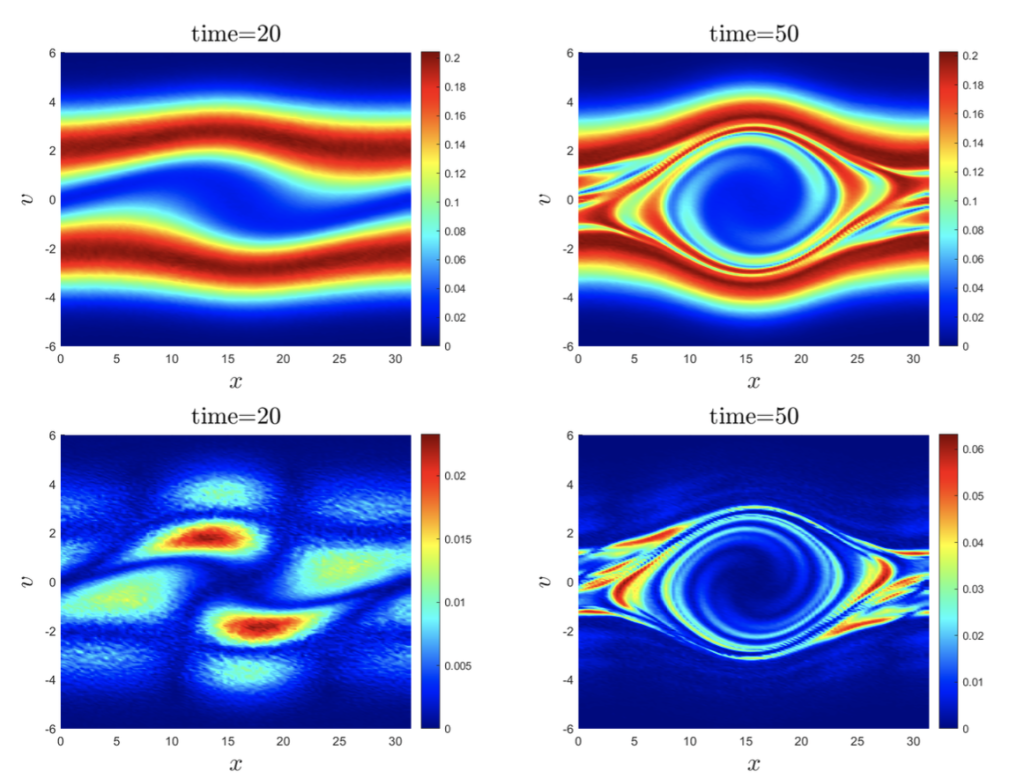
The design of particle simulation methods for collisional plasma physics has always represented a challenge due to the unbounded total collisional cross section, which prevents a natural extension of the classical Direct Simulation Monte Carlo (DSMC) method devised for the Boltzmann equation.
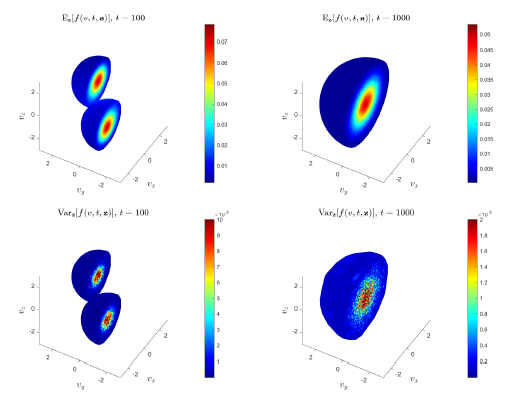
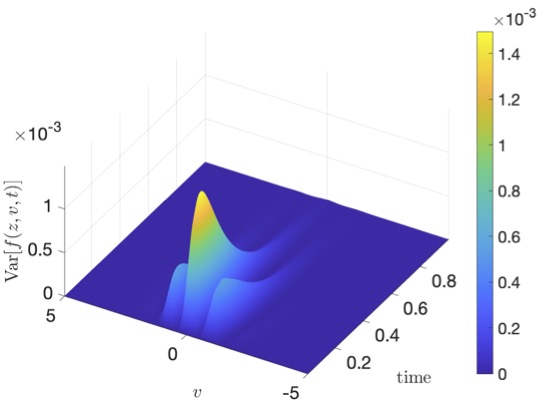
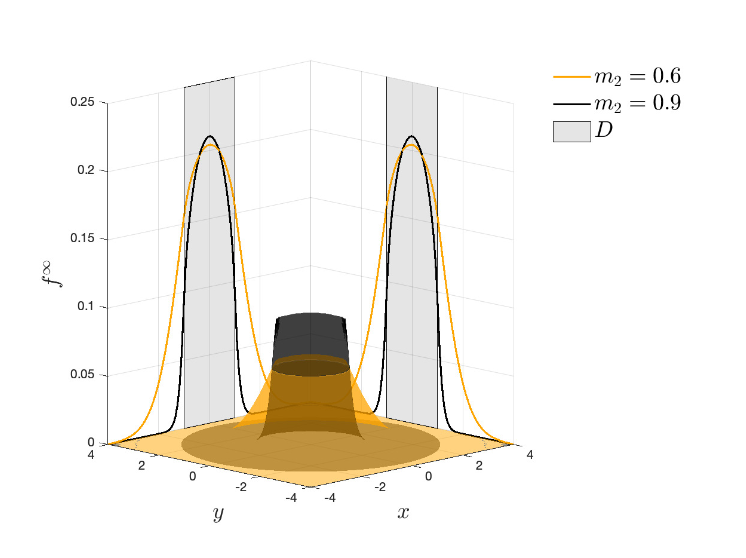
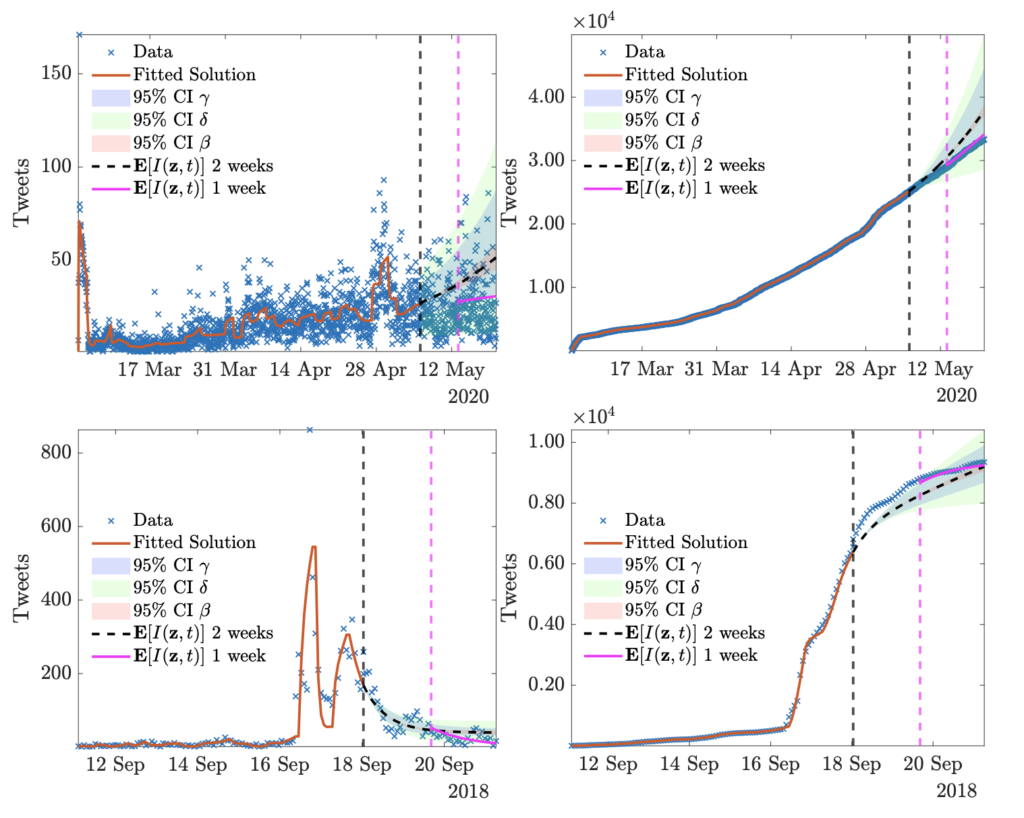
One way to overcome this problem is to consider the design of Monte Carlo algorithms that are robust in the so-called grazing collision limit. In the first part of this manuscript, we will focus on the construction of collision algorithms for the Landau-Fokker-Planck equation based on the grazing collision asymptotics and which avoids the use of iterative solvers. Subsequently, we discuss problems involving uncertainties and show how to develop a stochastic Galerkin projection of the particle dynamics which permits to recover spectral accuracy for smooth solutions in the random space. Several classical numerical tests are reported to validate the present approach.